一文讲通 React 的 diff 过程

发表于 更新于 分类于

看完这篇文章，我们可以弄明白下面这几个问题：

  1. 传统diff 算法的瓶颈是什么？
  2. React 的 diff 算法是怎么实现的？
  3. React 的 diff 算法发生在哪个阶段？
  4. React 的元素的 key 是做什么的？
  5. React 是怎么通过 key 实现高效 diff 的？

Fiber 节点的构建

下面的伪代码展示了 fiber 构建的过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function workLoop(deadline) {
  // requestIdleCallback 给 shouldYield 赋值，告诉我们浏览器是否空闲
  let shouldYield = false
  while (nextUnitOfWork && !shouldYield) {
    nextUnitOfWork = performUnitOfWork(nextUnitOfWork)
    shouldYield = deadline.timeRemaining() < 1
  }
  // 循环调用 workLoop
  requestIdleCallback(workLoop)
}

requestIdleCallback(workLoop)

// 构建完当前 fiber 节点后，会返回下一个待构建的节点 如：fiber.sibling、fiber.parent...
function performUnitOfWork(nextUnitOfWork) {
  // TODO
}
  • 不熟悉 requestIdleCallback 可以点这里查看，这个方法很简单：它需要传入一个 callback，浏览器会在空闲时去调用这个 callback，然后给这个 callback 传入一个 IdleDeadline，IdleDeadline 会预估一个剩余闲置时间，我们可以通过还剩多少闲置时间去判断，是否足够去执行下一个单元任务。
  • performUnitOfWork 方法将传入的节点创建为 Fiber ，然后返回下一个待构建的节点并赋值给 nextUnitOfWork，同时还会将刚创建的 fiber 与已创建的 fiber 连接起来构成 Fiber 树。

performUnitOfWork 的工作可以分为两部分：“递”和“归”。

render 阶段

render 阶段的开始，首先从 rootFiber 开始向下深度优先遍历，也就是不断 while 循环执行 performUnitOfWork，会经历递和归两个阶段。

“递”阶段

  • 向下遍历，每个遍历到的 Fiber 节点会调用 beginWork 方法。
  • 该方法会根据传入的 Fiber 节点创建子Fiber 节点，并将这两个 Fiber 节点连接起来。
  • 当遍历到没有 child 的节点时就会进入“归”阶段。

“归”阶段

  • 在“归”阶段会调用 completeWork 处理 Fiber 节点。
  • 当某个 Fiber 节点执行完 completeWork，如果其存在兄弟Fiber节点，会进入其兄弟Fiber的“递”阶段。
  • 如果不存在兄弟Fiber，会进入父Fiber的“归”阶段。

递和归举例

1
2
3
4
5
6
7
8
9
10
function App() {
  return (
    <div>
      i am
      <span>KaSong</span>
    </div>
  )
}

ReactDOM.render(<App />, document.getElementById("root"));

对应的 Fiber 树结构：

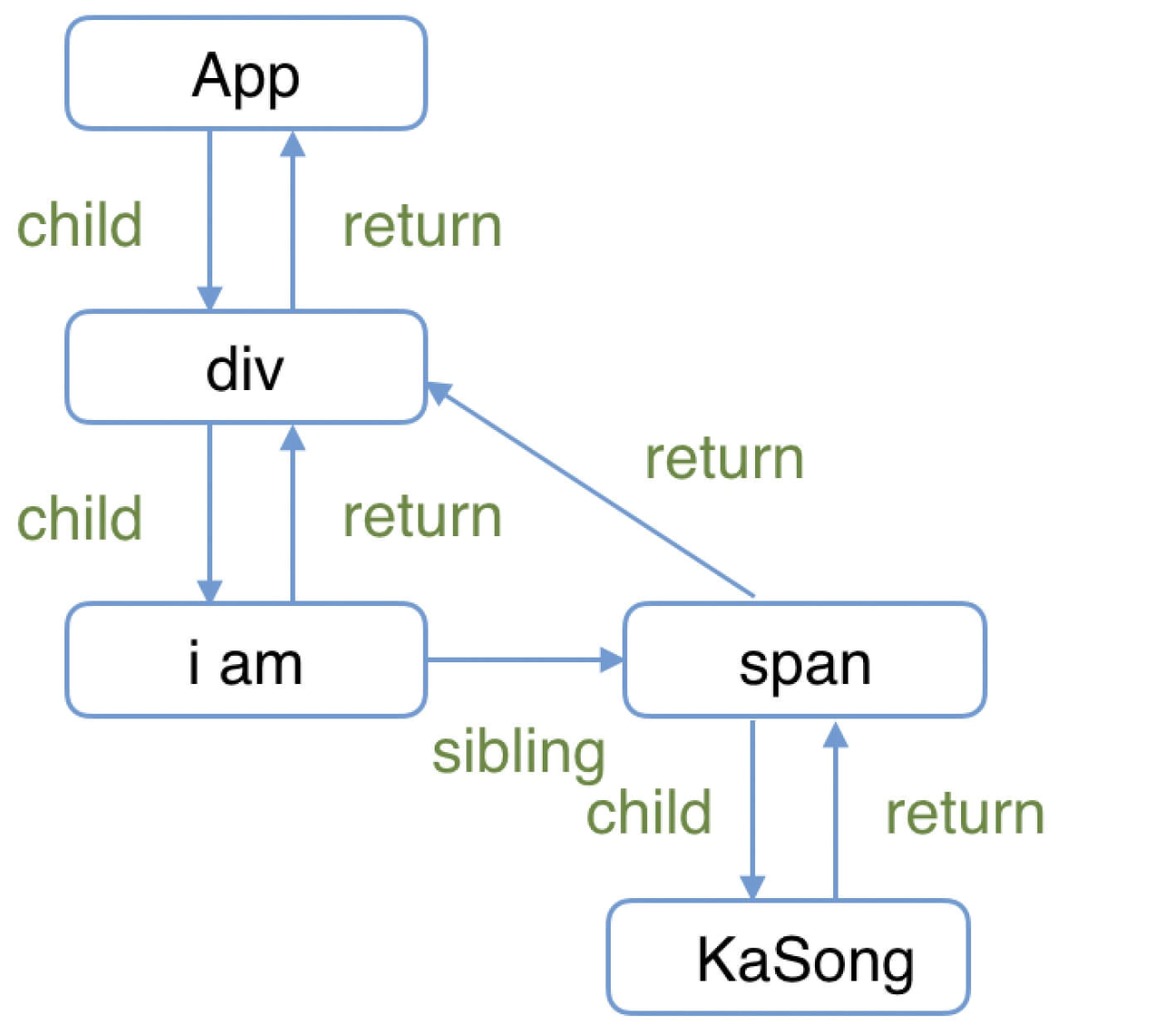
render 阶段会依次执行：

1
2
3
4
5
6
7
8
9
10
1. rootFiber beginWork
2. App Fiber beginWork
3. div Fiber beginWork
4. "i am" Fiber beginWork
5. "i am" Fiber completeWork
6. span Fiber beginWork
7. span Fiber completeWork
8. div Fiber completeWork
9. App Fiber completeWork
10. rootFiber completeWork

注意：之所以没有“KaSong”Fiber 的 beginWork/completeWork，是因为作为一种性能优化手段，针对只有单一文本子节点的 Fiber，React 会特殊处理。

render 完成

“递”和“归”阶段会交错执行直到“归”到 rootFiber。至此，render 阶段的工作就结束了。

Diff

diff 算法发生在两个阶段，分别是 beginWork 和 completeWork 阶段。

Diff 的瓶颈以及 React 如何应对

由于 Diff 操作本身也会带来性能损耗，React 文档中提到，即使在最前沿的算法中，将前后两棵树完全比对的算法的复杂程度为 O(n 3 )，其中 n 是树中元素的数量。
如果在 React 中使用了该算法，那么展示 1000 个元素所需要执行的计算量将在十亿的量级范围。这个开销实在是太过高昂。
为了降低算法复杂度，React 的 diff 会预设三个限制：

  1. 只进行同层比较。
  2. 新、旧节点的 type 不同，直接删除旧节点，创建新节点。如：元素由 div 变为 p，React会销毁div及其子孙节点，并新建p` 及其子孙节点。
  3. 通过 key 来复用节点。

所以 react 中 diff 算法主要遵循上面的三个层级的策略：

  1. tree 层级
  2. conponent 层级
  3. element 层级

tree 层级

DOM 节点跨层级的操作不做优化，只会对相同层级的节点进行比较

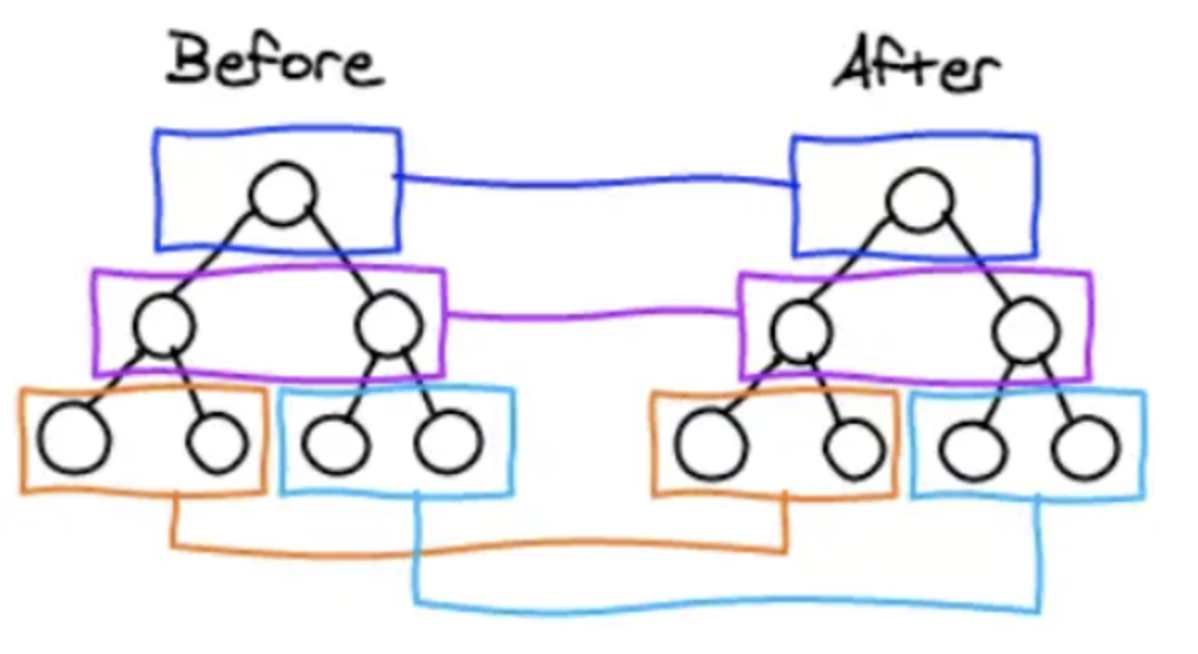
只有删除、创建操作，没有移动操作，如下图：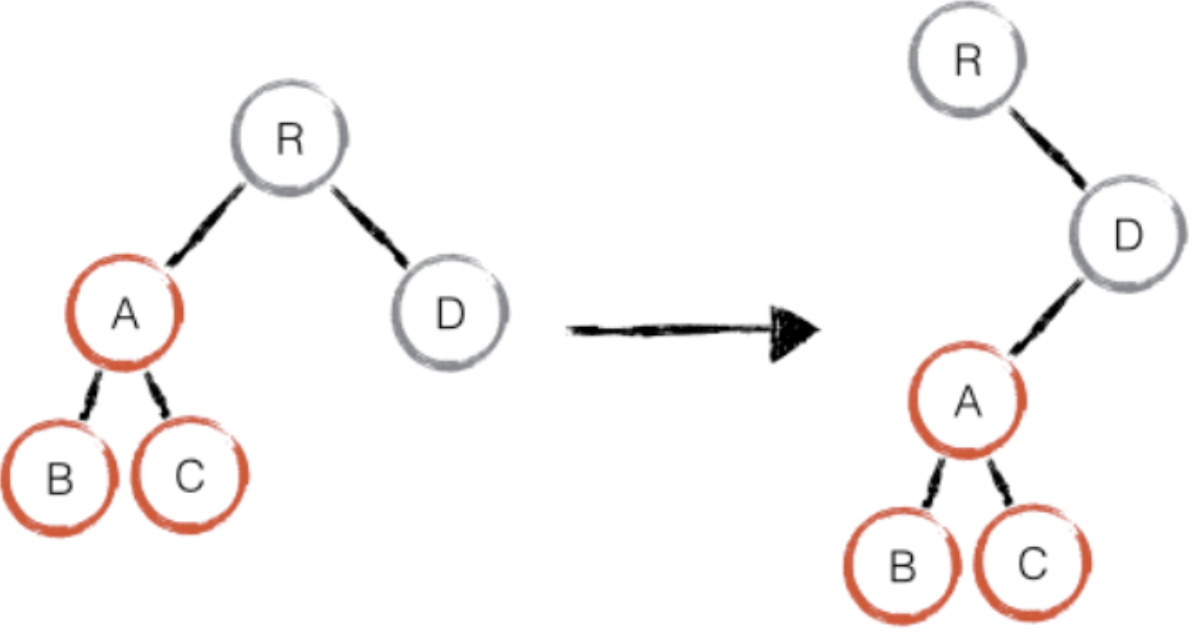

react 发现新树中，R 节点下没有了 A，那么直接删除 A，在 D 节点下创建 A 以及下属节点，上述操作中，只有删除和创建操作

component 层级

如果是同一个类的组件，则会继续往下 diff 运算，如果不是一个类的组件，那么直接删除这个组件下的所有子节点，创建新的

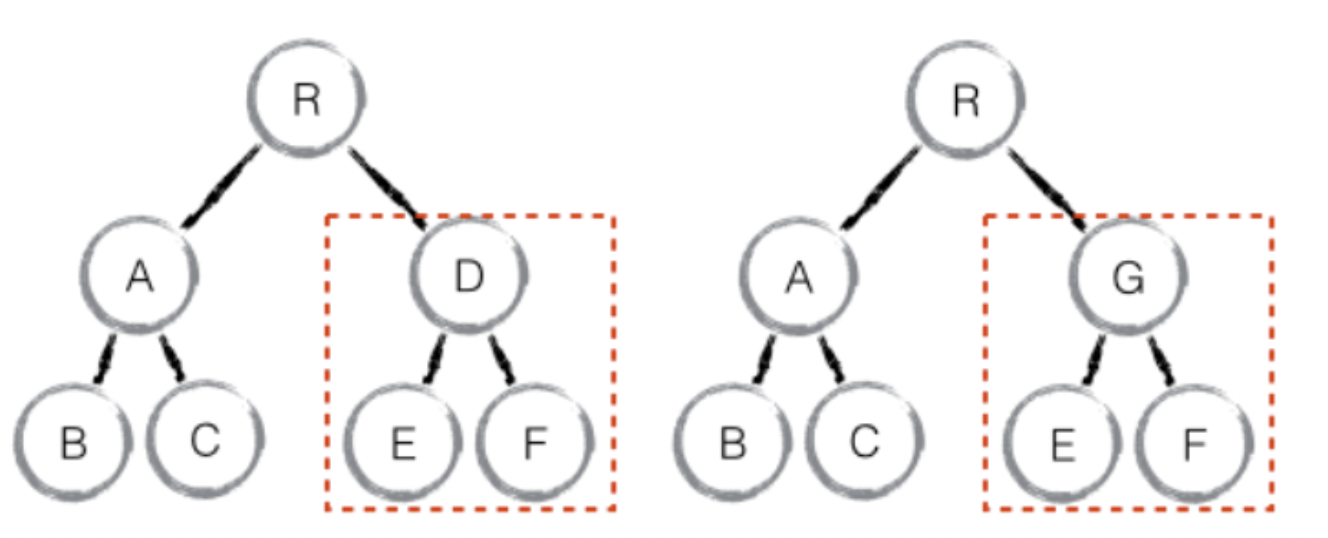
当 component D 换成了 component G 后，即使两者的结构非常类似，也会将 D 删除再重新创建 G

element 层级

对于比较同一层级的节点们，每个节点在对应的层级用唯一的 key 作为标识

提供了 3 种节点操作，分别为 INSERT_MARKUP(插入)、MOVE_EXISTING (移动) 和 REMOVE_NODE (删除)

如下场景：

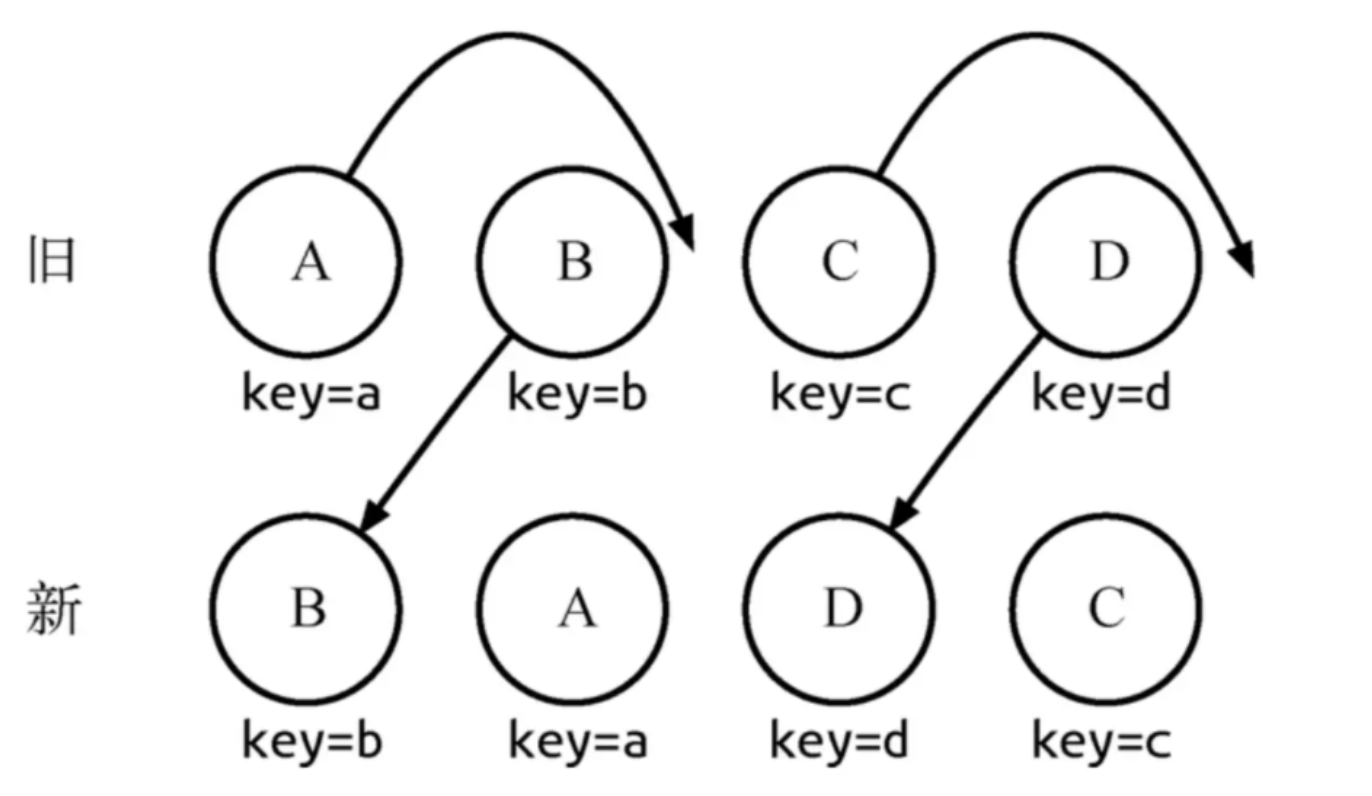
通过 key 可以准确地发现新旧集合中的节点都是相同的节点，因此无需进行节点删除和创建，只需要将旧集合中节点的位置进行移动，更新为新集合中节点的位置

Diff 是如何实现的

我们从 Diff 的入口函数 reconcileChildFibers 出发，该函数会根据 newChild（即 JSX 对象）类型调用不同的处理函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 根据 newChild 类型选择不同 diff 函数处理
function reconcileChildFibers(
  returnFiber: Fiber,
  currentFirstChild: Fiber | null,
  newChild: any,
): Fiber | null {

  const isObject = typeof newChild === 'object' && newChild !== null;

  if (isObject) {
    // object 类型，可能是 REACT_ELEMENT_TYPE 或 REACT_PORTAL_TYPE
    switch (newChild.$$typeof) {
      case REACT_ELEMENT_TYPE:
        // 调用 reconcileSingleElement 处理
      // // ...省略其他 case
    }
  }

  if (typeof newChild === 'string' || typeof newChild === 'number') {
    // 调用 reconcileSingleTextNode 处理
    // ...省略
  }

  if (isArray(newChild)) {
    // 调用 reconcileChildrenArray 处理
    // ...省略
  }

  // 一些其他情况调用处理函数
  // ...省略

  // 以上都没有命中，删除节点
  return deleteRemainingChildren(returnFiber, currentFirstChild);
}

我们可以从同级的节点数量将 Diff 分为两类：

  • 当 newChild 类型为 object、number、string，代表同级只有一个节点
  • 当 newChild 类型为 Array，同级有多个节点

在接下来两节我们会分别讨论这两类节点的 Diff

单节点 diff

对于单个节点，我们以类型 object 为例，会进入 reconcileSingleElement

1
2
3
4
5
6
7
8
9
10
const isObject = typeof newChild === 'object' && newChild !== null;

  if (isObject) {
    // 对象类型，可能是 REACT_ELEMENT_TYPE 或 REACT_PORTAL_TYPE
    switch (newChild.$$typeof) {
      case REACT_ELEMENT_TYPE:
        // 调用 reconcileSingleElement 处理
      // ...其他 case
    }
  }

React 通过先判断 key 是否相同，如果 key 相同则判断 type 是否相同，只有都相同时一个 DOM 节点才能复用。

这里有个细节需要关注下：

  • 当 key 相同且 type 不同时，执行 deleteRemainingChildren 将 child 及其兄弟 fiber 都标记删除。

  • 当 key 不同时仅将 child 标记删除 (后面还有兄弟 fiber 还没有遍历到。所以仅仅标记该 fiber 删除。)

考虑如下例子：当前页面有 3 个 li，我们要全部删除，再插入一个 p。

1
2
3
4
5
// 当前页面显示的
ul > li * 3

// 这次需要更新的
ul > p
  • 由于检测新节点只有一个 p，属于单节点比较。
  • 在 reconcileSingleElement 中遍历之前的 3 个 fiber（对应的 DOM 为 3 个 li），寻找本次更新的 p 是否可以复用之前的 3 个 fiber 中某个的 DOM。
  • 当 key 相同且 type 不同时，代表我们已经找到本次更新的 p 对应的上次的 fiber，但是 p 与 li type 不同，不能复用。既然唯一的可能性已经不能复用，则剩下的 fiber 都没有机会了，所以都需要标记删除。
  • 当 key 不同时只代表遍历到的该 fiber 不能被 p 复用，后面还有兄弟 fiber 还没有遍历到。所以仅仅标记该 fiber 删除

多节点 diff

这种情况下，reconcileChildFibers 的 newChild 参数类型为 Array，在 reconcileChildFibers 函数内部对应如下情况：

1
2
3
4
if (isArray(newChild)) {
    // 调用 reconcileChildrenArray 处理
    // ...省略
  }

然后归纳要处理的情况：

  1. 节点更新
  2. 节点新增或减少
  3. 节点位置变化

同级多个节点的 Diff，一定属于以上三种情况中的一种或多种。

diff 思路

该如何设计算法呢？如果让我设计一个 Diff 算法，我首先想到的方案是：

  1. 判断当前节点的更新属于哪种情况
  2. 如果是新增，执行新增逻辑
  3. 如果是删除，执行删除逻辑
  4. 如果是更新，执行更新逻辑

按这个方案，其实有个隐含的前提——不同操作的优先级是相同的

但是 React 团队发现，在日常开发中，相较于新增和删除，更新组件发生的频率更高。所以 Diff 会优先判断当前节点是否属于更新。

为什么不能用双指针遍历

在我们做数组相关的算法题时，经常使用双指针从数组头和尾同时遍历以提高效率，但是这里却不行。

虽然 newChildren 为数组形式，但是老节点是 fiber链表，同级的 Fiber 节点是由 sibling 指针链接形成的单链表，即不支持双指针遍历。即 newChildren[0]与fiber比较，newChildren[1]与fiber.sibling比较。

所以无法使用双指针优化，基于以上原因，Diff 算法的整体逻辑会经历两轮遍历：

  • 第一轮遍历：处理更新的节点。
  • 第二轮遍历：处理剩下的不属于更新的节点。

第一轮遍历

第一轮遍历步骤如下：

  1. let i = 0，遍历 newChildren，将 newChildren[i]与oldFiber比较，判断 DOM 节点是否可复用。
  2. 如果可复用，i++，继续比较 newChildren[i]与oldFiber.sibling，可以复用则继续遍历。
  3. 如果不可复用，分两种情况：
    • key 不同导致不可复用，立即跳出整个遍历，第一轮遍历结束。
    • key 相同 而type 不同导致不可复用，会将 oldFiber 标记为 DELETION，并继续遍历
  4. 如果 newChildren 遍历完（即 i === newChildren.length - 1）或者 oldFiber 遍历完（即 oldFiber.sibling === null），跳出遍历，第一轮遍历结束。

当遍历结束后，会有两种结果：

步骤 3 跳出的遍历

此时 newChildren 没有遍历完，oldFiber 也没有遍历完。

举个例子，考虑如下代码：

1
2
3
4
5
6
7
8
9
// 之前
<li key="0">0</li>
<li key="1">1</li>
<li key="2">2</li>
            
// 之后
<li key="0">0</li>
<li key="2">1</li>
<li key="1">2</li>

第一个节点可复用，遍历到 key === 2 的节点发现 key 改变，不可复用，跳出遍历，等待第二轮遍历处理。

此时 oldFiber 剩下 key === 1、key === 2 未遍历，newChildren 剩下 key === 2、key === 1 未遍历。

步骤 4 跳出的遍历

可能 newChildren 遍历完，或 oldFiber 遍历完，或他们同时遍历完。

举个例子，考虑如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 之前
<li key="0" className="a">0</li>
<li key="1" className="b">1</li>
            
// 之后 情况 1 —— newChildren 与 oldFiber 都遍历完
<li key="0" className="aa">0</li>
<li key="1" className="bb">1</li>
            
// 之后 情况 2 —— newChildren 没遍历完，oldFiber 遍历完
// newChildren 剩下 key==="2" 未遍历
<li key="0" className="aa">0</li>
<li key="1" className="bb">1</li>
<li key="2" className="cc">2</li>
            
// 之后 情况 3 —— newChildren 遍历完，oldFiber 没遍历完
// oldFiber 剩下 key==="1" 未遍历
<li key="0" className="aa">0</li>

带着第一轮遍历的结果，我们开始第二轮遍历。

第二轮遍历

对于第一轮遍历的结果，我们分别讨论：

  1. newChildren 与 oldFiber 同时遍历完

那就是最理想的情况：只需在第一轮遍历进行组件更新。此时 Diff 结束。

  1. newChildren 没遍历完，oldFiber 遍历完

已有的 DOM 节点都复用了，这时还有新加入的节点，意味着本次更新有新节点插入，我们只需要遍历剩下的 newChildren 为生成的 fiber 依次标记 Placement。

  1. newChildren 遍历完，oldFiber 没遍历完

意味着本次更新比之前的节点数量少，有节点被删除了。所以需要遍历剩下的 oldFiber，依次标记 Deletion。

  1. newChildren 与 oldFiber 都没遍历完

这意味着有节点在这次更新中改变了位置。

这是 Diff 算法最精髓也是最难懂的部分。我们接下来会重点讲解。

处理移动的节点

移动的思想：如果当前节点在新集合中的位置比老集合中的位置靠前的话，是不会影响后续节点操作的，这时候不用动

操作过程中只比较 oldIndex 和 maxIndex，规则如下：

  • 当 oldIndex>maxIndex 时，将 oldIndex 的值赋值给 maxIndex
  • 当 oldIndex=maxIndex 时，不操作
  • 当 oldIndex<maxIndex 时，将当前节点移动到 index 的位置

即：遍历新节点，每个新节点有 2 个 index，一个是在旧节点的位置，另一个是遇到的最大旧节点的位置，然后根据上面判断决定旧节点是否右移。

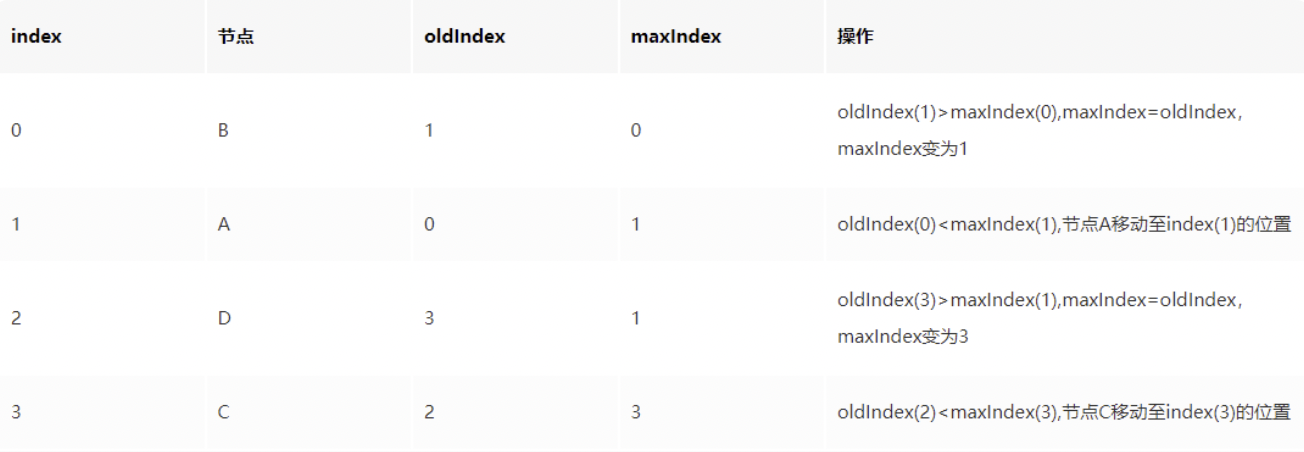
还是举上面的例子

diff 过程如下：

  1. 节点 B：此时 maxIndex=0，oldIndex=1；满足 maxIndex< oldIndex，因此 B 节点不动，此时 maxIndex= Math.max(oldIndex, maxIndex)，就是 1
  2. 节点 A：此时 maxIndex=1，oldIndex=0；不满足 maxIndex< oldIndex，因此 A 节点进行移动操作，此时 maxIndex= Math.max(oldIndex, maxIndex)，还是 1
  3. 节点 D：此时 maxIndex=1, oldIndex=3；满足 maxIndex< oldIndex，因此 D 节点不动，此时 maxIndex= Math.max(oldIndex, maxIndex)，就是 3
  4. 节点 C：此时 maxIndex=3，oldIndex=2；不满足 maxIndex< oldIndex，因此 C 节点进行移动操作，当前已经比较完了

当 ABCD 节点比较完成后，diff 过程还没完，还会整体遍历老集合中节点，看有没有没用到的节点，有的话，就删除

总结

  • 传统 diff 算法通过循环递归对节点进行依次对比，复杂度过高，为了降低算法复杂度，diff 遵循了 3 个层级的优化策略：
    1. 只进行同层比较。
    2. 新、旧节点的 type 不同，直接删除旧节点，创建新节点。
    3. 通过 key 来复用节点。
  • 从 Diff 的入口函数 reconcileChildFibers 出发，判断子元素的类型，若不是数组进入单节点diff，否则进入多节点diff
  • 单节点diff：先判断 key 是否相同，
    • 如果 key 相同，再看 type
      • type 相同，复用；
      • type 不同，全部删掉（包括它和它的兄弟元素，因为既然 key 一样，唯一的可能性都不能复用，则剩下的 fiber 都没有机会了）；
    • 如果 key 不同，只删除该child，再找到它的兄弟节点（child.silbing）的 key，直到找到key相同的节点，再同上操作
  • 多节点diff：归纳只有 3 种情况，更新节点、增减节点、位置变化，由于是单向的链表（newChildren[0]与fiber比较，newChildren[1]与fiber.sibling比较），所以不能像 vue 一样用双指针遍历，所以这里逻辑要经过两轮遍历：
    • 第一轮遍历：比较 key，
      • 可复用，继续遍历 (新节点 i++，老节点child.silbing)，
      • 不可复用，就停止第一轮遍历，进入第二轮遍历，有 2 种不可复用的情况：
          1. key 不同，直接停止
          1. key 相同，type 不同，标记删除，停止
    • 第二轮遍历：
      • 老节点遍历完了，新节点还有，则将剩下的新节点插入
      • 新节点遍历完了，老节点还有，则将剩下的老节点删除
      • 新老节点都还有，则移动顺序，这是 diff 算法最精髓也是最难懂的部分，规则：遍历新节点，每个新节点有 2 个 index，一个 index 表示它在旧节点的位置，另一个 index 表示遍历中遇到的最大旧节点的位置，用 oldIndex 和 maxIndex 表示
        • 当 oldIndex>maxIndex 时，将 oldIndex 的值赋值给 maxIndex
        • 当 oldIndex=maxIndex 时，不操作
        • 当 oldIndex<maxIndex 时，将当前节点移动到 index 的位置

参考：

  1. React 技术揭秘
  2. 面试官：说说你对 React diff 的理解？原理是什么？
  3. React 源码系列之八：React 的 diff 算法
  4. 有 React fiber，为什么不需要 Vue fiber？